题目描述
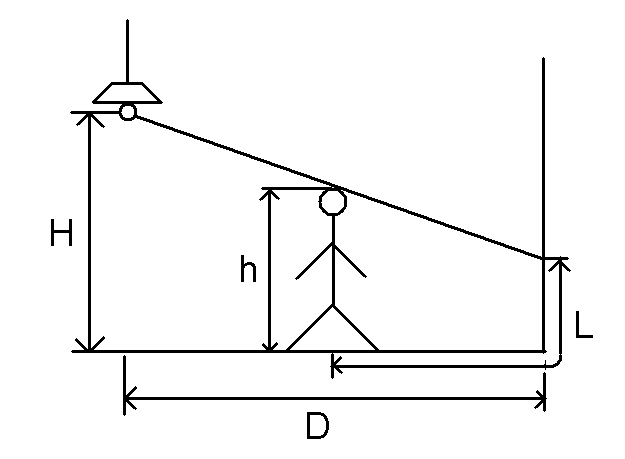
相比 Wildleopard 的家,他的弟弟 Mildleopard 比较穷。他的房子是狭窄的,而且在他的房间里仅有一个灯泡。每天晚上,他徘徊在自己狭小的房子里,思考如何赚更多的钱。有一天,他发现他的影子的长度随着他在灯泡和墙壁之间走动时会发生变化。一个突然的想法出现在他的脑海里,他想知道在房间里他的影子的最大长度。
输入格式
输入文件的第一行包含一个整数 T,表示测试数据的组数。
对于每组测试数据仅有一行包含三个实数 H,h 和 D,H 表示灯泡的高度,h 表示 Mildleopard 的身高,D 表示灯泡和墙的水平距离。
输出格式
输出文件共 T 行,每组数据占一行,表示影子的最大长度 L。当你的输出与标准输出的绝对误差不超过 10^−3 即视作通过。
输入输出样例
输入
3 2 1 0.5 2 0.5 3 4 3 4
输出
1.000 0.750 4.000
求最值的话,用分治最好,枚举人与墙之间的距离,算出最大值,这道题的话,讲一下三分做法
三分枚举很简单,几乎就是个模版,但是这道题要怎么算影子长度呢?
首先,我们先来确定一下距墙距离x的范围
最大肯定是D,已经紧贴墙壁了
最小是在影子刚好到墙角的那一刻,因为再前就只会小不会大了
可以看出,这一刻,灯高度H比上D,等于人高度d比影子长(人距墙的距离)
那么,最小的范围就是D-(D*h)/H
但是到这里,我们还是不知道影子长怎么求
先画个图
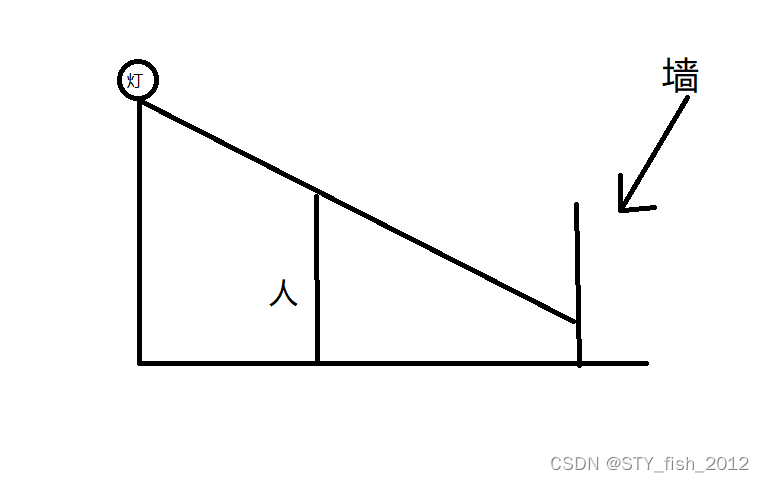
然后我们画两条神奇的辅助线

然后我用不同颜色标出来的这两个三角形,是相似三角形
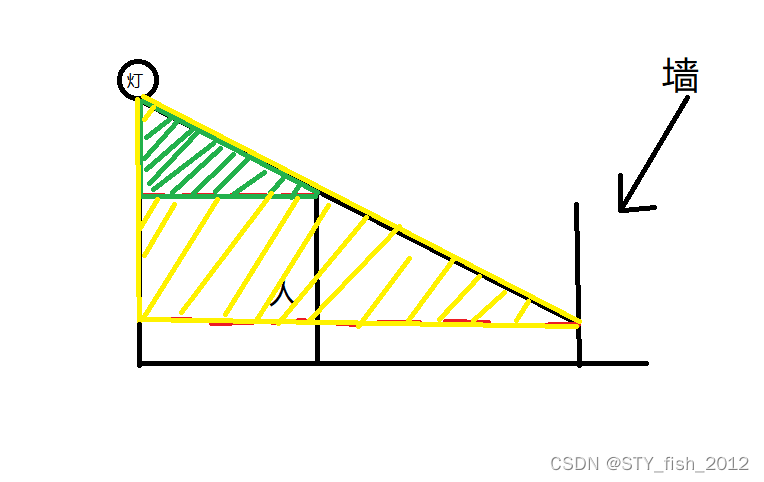
既然是相似三角形,那么任意两条边比值相等,所以这样就可以求出影子长度了
我们只需要用这种方法,算出墙上影子长度(刚好到墙角时,墙上影子长度为零),再加上地上影子长度(人与墙的距离),就能算出影子长度了
话不多说,代码奉上
#include<bits/stdc++.h>
using namespace std;
typedef double db;
int T;
db H,h,d;
db sum(db x){
return (d-x)+H-((H-h)/x*d);//计算影子长度
}
signed main(){
scanf("%d",&T);
while(T--){
scanf("%lf%lf%lf",&H,&h,&d);
db eps=1e-9;
db l=d-d*h/H,r=d;
db sum1,sum2;
while(r-l>eps){//三分
db mid1=l+(r-l)/3.0;
db mid2=r-(r-l)/3.0;
sum1=sum(mid1),sum2=sum(mid2);
if(sum1>sum2)r=mid2;
else l=mid1;
}
printf("%.3lf\n",sum1);
}
}